In der System Dynamics Community wird schon lange die Nützlichkeit von Causal Loop Diagrams (CLD) – zu Deutsch etwa „Wirkungsnetzwerke“ – diskutiert. Hier fragt Tom Fiddaman Are causal loop diagrams useful? Dabei geht es nicht darum, die Methode der Causal Loop Diagrams anzuzweifeln, sondern darum, gleich einen Schritt weiterzugehen und von Anfang an Stock-Flow-Modelle zu bauen. Dagegen spricht jedoch, dass Stock-Flow-Modelle ungleich schwieriger und aufwändiger sind als CLD. Diese sind dafür handlich und schnell entwickelt.
Pfeile sind Funktionen!
Gerade das ist der Kritikpunkt. Weil CLD sofort einleuchten – Parameter, die sich beeinflussen, sind mit einem Pfeil verbunden – meint schnell einer, er könne drauflos zeichnen. Das führt dann dazu, dass in der Literatur wirre CLD auftauchen, die die Kritik geradezu herausfordern.
Auf der anderen Seite betrachten auch die Kritker CLD nicht als das, was sie wirklich sind: verkettete reellwertige monotone Funktionen. Den Kritikern – das sind meist die ganz grossen der Szene, wie eben Tom Fiddaman, Kim Warren, George P. Richardson – ist dann jedes Argument recht, wenn es gilt, CLD zu umgehen, um gleich von Anfang an Stock-Flow-Modelle zu entwickeln. Nur: das ist nicht praxisgerecht! Gerade KMU haben kein Budget zur Entwicklung aufwändiger Stock-Flow-Diagramme.
Fiddaman bezieht sich in seinem Artikel auf Problems in Causal Loop Diagrams Revisited von George P. Richardson. Richardson macht dort das Beispiel eines Epidemiemodells, in dem ein Pfeil positiver Polarität „Infection rate –> sick population“ vorkommt. Dazu schreibt er:
[This arrow is false]. The link from the Infection rate to the Sick population has a similar problem:
when the infection rate decreases, the sick population does not decrease (move in the same direction) as the “S” label suggests — it would continue to increase. We know very well the reason for these behaviors: the infection rate always subtracts from the susceptible population and adds to the sick population. The populations are stocks, and the infection rate drains one stock and pours into the other
Richardson ist als Professor of Public Administration and Policy vermutlich kein Mathematiker. Er beachtet deshalb nicht, dass hier der funktionale Zusammenhang nicht von der Zeit abhängt. Zwar nimmt zeitlich die Grösse der infizierten Bevölkerung auf jeden Fall zu, auch wenn die Infektionsrate sinkt, da hat er recht. Aber das ist hier nicht die Frage. Es geht hier nicht um einen funktionalen Zusammenhang mit der Zeit, sondern mit der Infektionsrate. Wenn die Infektionsrate sinkt, sinkt selbstverständlich auch die Grösse der infzierten Bevölkerung.
Ein Pfeil ist meist keine Funktion der Zeit
Um das einzusehen, schauen wir die Welt zunächst durch Richardsons Augen an. Er hat recht, dass die infizierte Bevölkerung ein Bestand ist und die Infektionsrate angibt, wie viel Prozent der „ansteckbaren“ Bevölkerung krank werden. Das hat ungefähr dieselbe Dynamik, wie ein Zinsmodell. Sind i1 < i2 < i3 drei verschiedene Infektionsraten, dann sieht die Dynamik der infizierten Bevölkerung so aus:
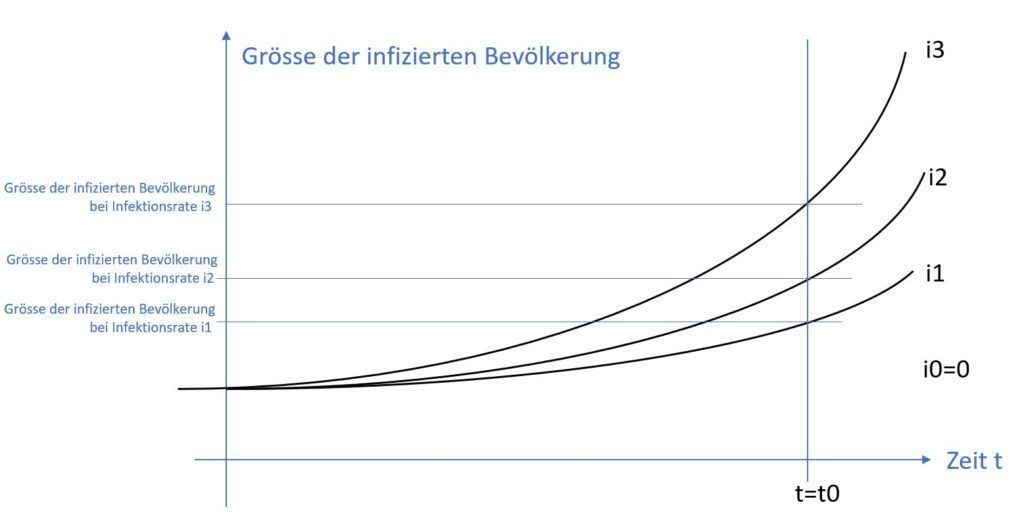
In der Tat nimmt jede dieser Funktionen zu, auch wenn die Infektionrate sinkt, z.B. i2 nach i1: die infizierte Bevölkerung wächst auch bei i1. Aber das ist hier gar nicht die Frage!
Der Pfeil „Infection rate –> sick population“ ist eine monoton steigende Funktion der Infektionsrate, die einem Wert der Infektionsrate eine Anzahl infizierte Menschen zuordnet.
Wir müssen also in der obigen Grafik einen bestimmten Zeitpunkt t0 festhalten und schauen, wie sich die infizierte Bevölkerung in Abhängigkeit der Infektionsrate verhält.
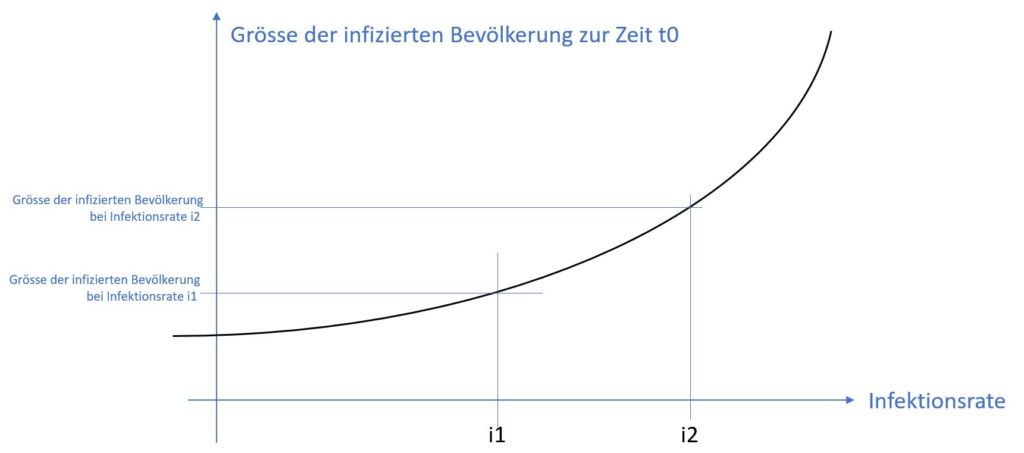
Wir sehen, dass das eine monoton steigende Funktion ist, d.h. wenn die Infektionsrate von i2 auf i1 sinkt, dann sinkt auch die dazu gehörende Anzahl infizierter Menschen.
CLD können weitgehende Einsichten vermitteln. Voraussetzung ist, dass sie sauber und präzise eingesetzt werden. Auch ein CLD ist bereits ein Modell! Es hilft bei der Kommunikation eines Sachverhalts und bei der Einschätzung von Fern- und Nebenwirkungen.
Loops machen die Essenz eines CLD aus!
Im Allgemeinen sind CLD zu umfangreich und die Bezeichnungen der Parameter sind suggestiv. Anfänger würden den Pfeil „Infection rate –> sick population“ in Richardsons CLD vielleicht so bezeichnen:
aggressive Infection –> epidemic increasing sick population
in der Meinung, plakative Bezeichnungen würden die Verantwortlichen eher zum Handeln bringen. Aber die Infektionsrate könnte auch niedrig und die Zunahme der infizierten Bevölkerung moderat sein. Deshalb sind neutrale Bezeichnung Voraussetzung brauchbarer CLD.
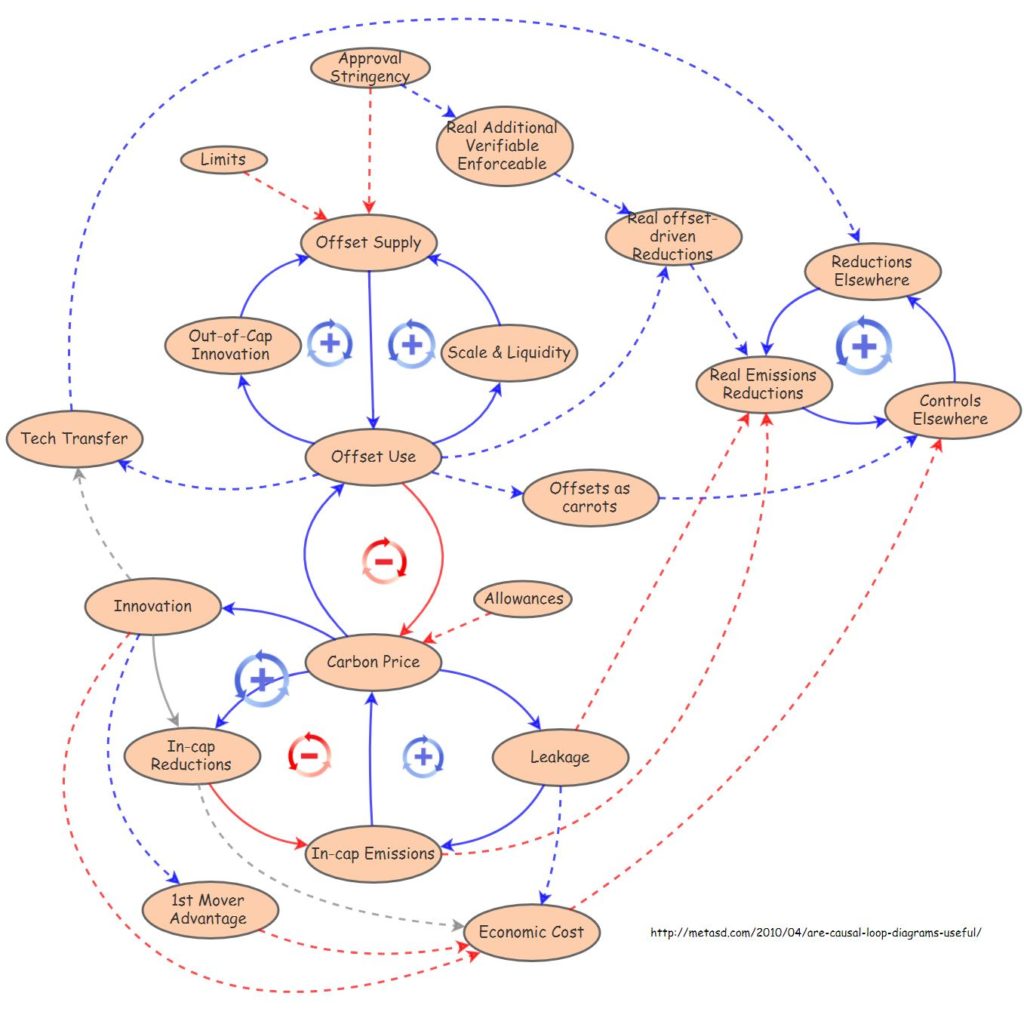
Wichtig sind die Loops in den CLD. Diese müssten deutlich sichtbar gemacht werden, denn nur sie tragen zur Dynamik bei. Im eingangs erwähnten Artikel stellt Tom Fiddaman ein CLD zur Verfügung, das er zusammen mit Ron Suiter über CO2-Emmissionen entwickelte.
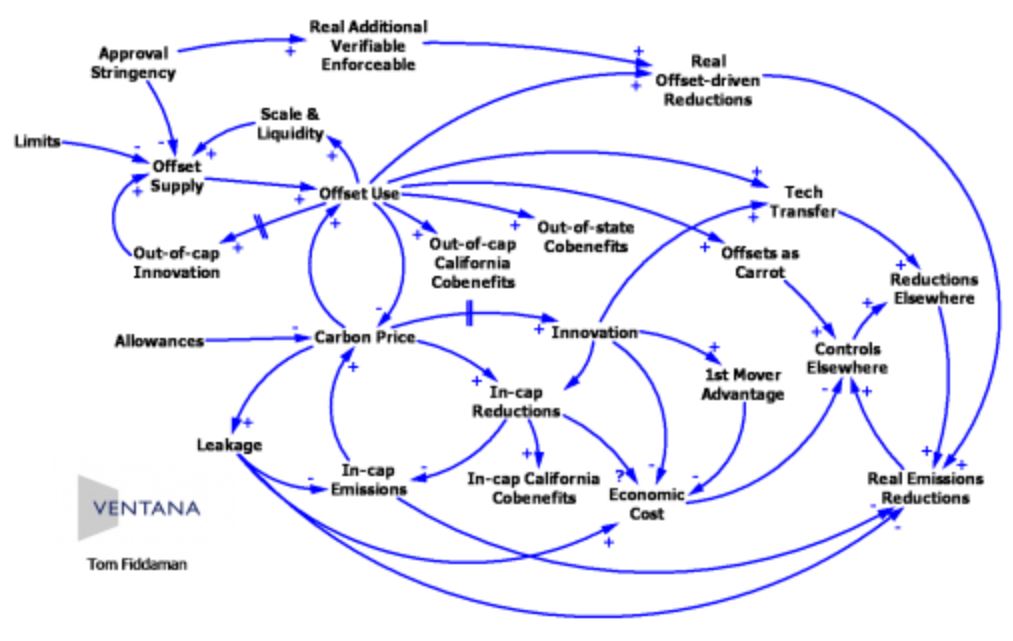
Da die beiden Profis sind, ist das CLD bereits auf einem hohen Niveau. Ich versuchte, ein wirklich wirres CLD zu finden, scheiterte aber an Copyrights. Das Vorgehen, um das es mir hier geht, kann auch am Fiddaman-CLD gezeigt werden. Nicht alle Loops sind direkt ersichtlich (und wenn, dann nehmen wir an, dass nicht). Ich habe das CLD zuerst in insightmaker.com möglichst so übernommen, wie es im Artikel steht. Die drei terminalen Grössen „Out-of-state Cobenefits“, „Out-of-cap California Cobenefits“ und „In-cap California Cobenefits“ habe ich weggelassen, denn sie tragen nichts zum System bei und sind bloss Ablesegrössen, wie ein Stromzähler. Wie üblich, haben blaue Pfeile positive Polarität und rote negative. Wenn Sie auf das Bild klicken, gelangen Sie gleich in den insightmaker.
(https://insightmaker.com/insight/97633/emissions-original)
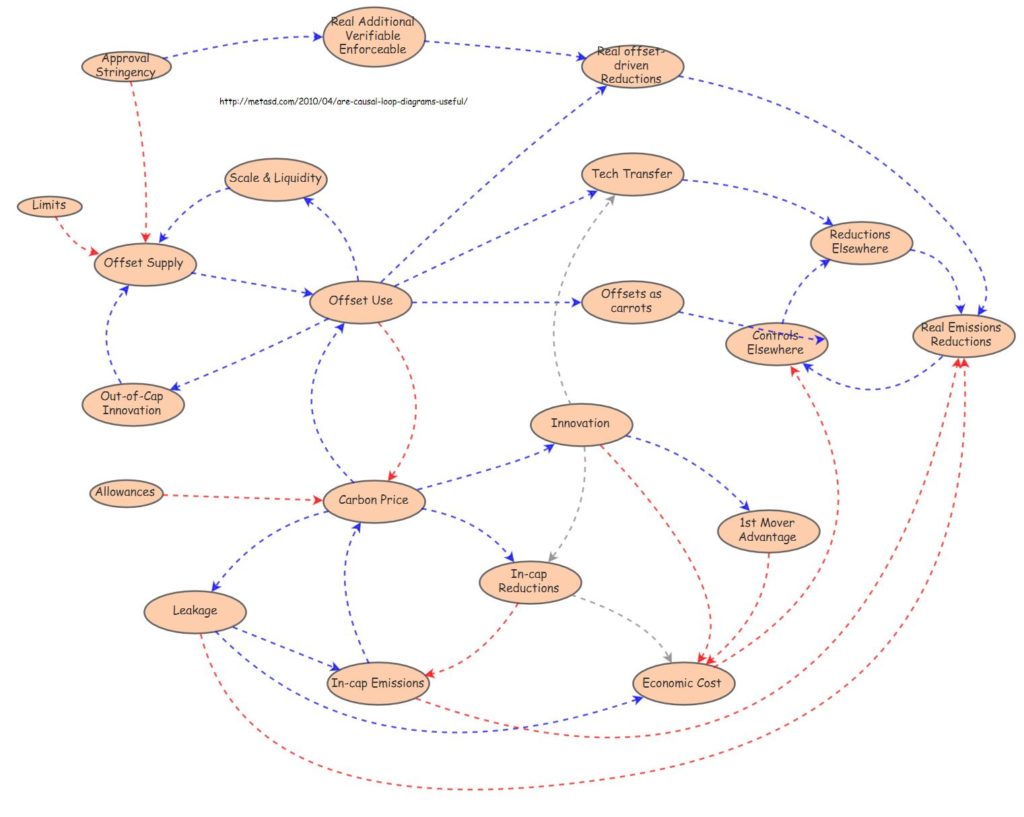
Dann habe ich mit Hilfe der Funktion „Identify loops“ die Kreise ausgemacht und sie in den Fokus des Diagramms geholt:
(https://insightmaker.com/insight/97711/emissions-kreise)
Erst in dieser Darstellung kommt die Nützlichkeit eines CLD zum Ausdruck: man sieht sogleich, dass der Kreis oben rechts vom übrigen System völlig isoliert ist. Wenn man sich nicht gerade für die drei Grössen, die diesen Kreis bilden – „Reductions Elsewhere“, „Real Emissions Reductions“ und „Control Elsewhere“ – interessiert, könnte man den Kreis sowie alle Pfeile, die zum Kreis hin führen, weglassen. Die Grössen, auf dem Weg zum Kreis, wie z.B. „Real Additional Verifiable Enforceable“ und „Real Offset-driven Reductions“ sind ebenfalls unnütz und reine Massumwandler.
Das CLD reduziert sich auf das System der sechs Kreise in der Mitte des Diagramms. Es sind vier reinforcing Loops und zwei balanced Loops. Meine Erfahrung zeigte, dass sich Kreise ähnlich wie Pfeile verhalten, wenn man die Zuordnung
reinforcing loop –> postivie Polarität
balanced loop –> negative Polarität
macht. Ein Kreis, in welchem eine gerade Anzahl Pfeile negativer Polarität vorkommt, ist reinforcing. Ein Kreissystem in welchem es eine gerade Anzahl balanced Kreise gibt, wäre demnach vermutlich im Gesamten reinforcing. Stimmt diese Vermutung, dann wird sich das Fiddaman-CLD gesamthaft aufschaukeln (oder kollabieren). Um diese Vermutung zu festigen, ist weitere Forschungsarbeit nötig.
Die Analyse der Kreisstruktur eines CLD macht dieses zu einem sehr nützlichen Werkzeug, aller Unkenrufe der Community zum Trotz.

Hallo Peter,
danke, dass Du Dich in den letzten Beiträgen so ausführlich mit diesem Thema beschäftigst.
Du weißt, dass ich in einigen Punkten nicht ganz bei Dir bin. Ich glaube nämlich ganz fest daran, dass selbst beim Zeichnen von CLDs eine Unterscheidung in „Bestand und Fluss“ unabdingbar ist. Warum? Weil Änderungen sich stets in Zeit und Raum vollziehen.
Ich mache es mal deutlich.
Du schreibst: „Es geht hier nicht um einen funktionalen Zusammenhang mit der Zeit, sondern mit der Infektionsrate. Wenn die Infektionsrate sinkt, sinkt selbstverständlich auch die Grösse der infizierten Bevölkerung.“
Es geht in CLDs Deiner Meinung nach nicht um den funktionalen Zusammenhang mit der Zeit. Okay, wenn dem so ist, dann benötigt man die Unterscheidung in Bestand und Fluss nicht. Fein.
Aber Deine Aussage „Wenn die Infektionsrate sinkt, sinkt selbstverständlich auch die Grösse der infizierten Bevölkerung.“ ist nicht immer richtig und einfach per Empirie nachzuvollziehen, auch ohne CLD. Da kann man nur mal eine Badewanne mit Wasser füllen und den Wasserhahn zudrehen aber eben nicht vollständig zu. Der Wasserstand in der Wanne nimmt nicht ab sondern zu. Aber laut CLD erhalte ich diese Aussage. Also wozu dann CLDs, wenn die Aussagen ohne Hinzunahme der Zeit falsch werden?
Das verstehe ich noch nicht ganz.
BG, Conny
Lies meine Ausführungen genau: die Funktion „Infektionsrate –> infizierte Bevölkerung“ ist monoton steigend! Verstehst Du das?
Wenn ich ein Kapital zu 1% anlege und Du denselben Betrag zu 2%, so ist mein Kapital zu einem bestimmten Zeitpunkt halt einfach kleiner als Deines. Die Funktion „Zinsrate –> Kapital“ ist monoton steigend. Wenn die Zinsrate sinkt, sinkt das Kapital *in einem bestimmten Zeitpunkt*.
Das gilt jedoch nicht für die durch die Zinsrate parametrisierte Funktion „Zeit –> Kapital“. Wenn die Zinsrate sinkt, nimmt diese Funktion dennoch zu. Aber diese Funktion kommt im CLD gar nicht vor, bzw. nur implizit.
Kannst Du dies beiden Funktionen unterscheiden?
Hallo Peter,
wie kommst Du darauf, dass ich nicht genau gelesen habe? Nur weil ich Deine Meinung nicht teile?
Deinen Erklärungen kann ich folgen und auch bejahen. Diese beziehen sich mathematisch immer auf einen bestimmten Zeitpunkt. Das heißt, das Modell in sich ist mathematisch stimmig und konsistent. In dem Moment aber, wo ich es auf andere Systeme außerhalb der Mathematik loslasse, fängt die Nichtpassfähigkeit an. Denn, was wurde hier exkludiert? Du sagst es selber. Die Dynamik, die Zeit also innerhalb der Funktion. Und damit wird das Modell des CLD für mich nicht passfähig. Denn Änderungen verlaufen in unserer Welt stets in Raum und Zeit ab.
Jedes Modell trivialisiert die Umwelt. Das muss so sein. Das Modell sollte also einfach sein, aber nicht ZU einfach. Und das ist in meinen Augen hier der Fall.
Woran erkenne ich das? Die Aussage „Wenn die Infektionsrate sinkt, sinkt selbstverständlich auch die Grösse der infizierten Bevölkerung.“ wird durch das Modell erzeugt. Diese Aussage ist aber per Empirie sehr einfach widerlegbar.
Nun könnte man natürlich behaupten, die Nutzung von CLDs ohne Zeitkomponente, um Erkenntnisse generieren zu können, ist nur ein erster Schritt. Weitere Schritte sollten folgen, nämlich die Hinzunahme der Betrachtung in Bestand und Fluss. Allerdings ist ein erster Schritt genau dann nicht gut, wenn er in die falsche Richtung verläuft, Und das tut er hier.
Bleiben wir beim obigen Satz. Mit dieser Erkenntnis und dem Ziel folgend, infizierte Menschen auf der Welt zu verringern, müsste man sich einzig und allein nur darum kümmern, keine neuen Infektionen zuzulassen. Man würde sich aber überhaupt nicht um die bereits infizierten Menschen kümmern und sie medizinisch versorgen. Falsche Handlung durch falsche Erkenntnis. Fatal.
Wie gesagt, das ist meine Sicht, für die ich auch keine Allgemeingültigkeit beanspruche. Ich habe nur gute Gründe für mich gefunden, CLD Modellierung ohne Betrachtung der Faktoren in Bestand und Fluss niemals durchzuführen.
BG, Conny
Nein, Mathematik gilt auch bei Infektionsraten, Badewannen und Zinseszinsen. Worum geht es Dir denn? Du siehst nur nicht ein, dass ein Zufluss positive Polarität hat? Aber dennoch wirst Du ja nicht abstreiten, dass ein Zinsmodell reinforcing ist. Kapital –> Zins –> Kapital schaukelt sich auch in Deiner Wahrnehmung auf, das beklagst Du ja oft. Der Zufluss Zins –> Kapital muss also positive Polarität haben. Und das kann ich eben erklären.
Einig sind wir, dass CLD nicht exakt sind. Mir geht es nur darum, die Ehre von CLD zu retten, indem ich sage, dass sie durchaus zu systemischen Einsichten führen können, wenn sie richtig angewendet werden. Für Dich bedeutet „richtig anwenden“ die Unterscheidung von Fluss- und Bestandesgrössen. Dagegen habe ich grundsätzlich nichts einzuwenden, wenn es das CLD nicht unnötig aufbläht. Z.B. habe ich kürzlich ein CLD gesehen, das „Hühner“ und „Eier“ in einen Kreis anordnete. Je mehr Hühner, desto mehr Eier und umgekehrt. Stimmt doch!? Aber hier werden die Flussgrössen „legen“ und „ausbrüten“ völlig unterdrückt. Dennoch würde mir das Diagramm zur Diskussion der Dynamik genügen.
Für mich steht dagegen die nicht suggestive Bezeichnung und die Konzentration auf Kreise im Mittelpunkt. Zusammen würden wir die besten CLD hervorbringen! 🙂
Moin Peter,
ich versuche meine Bedenken aus einer anderen Sicht zu begründen.
Die positive Polarität, die Du in Deinem Hühnerbeispiel bringst klappt genau deshalb so gut, weil Du die Zeit ausknipst und immer einen ganz konkreten Zeitpunkt des Flusses betrachtest, den Zufluss von Eiern. Der Bestand an Eiern bleibt hier aber außen vor.
Positive Polarität bedeutet ja nicht nur „Je mehr Hühner desto mehr Eier.“ sondern auch, wie Du schreibst „Je weniger Hühner desto weniger Eier.“ Und genau diese Erklärung passt nicht, wenn die Eier als Bestand gesehen werden.
Flussfaktoren haben keine Geschichte und damit keine Zeitkomponente in sich. Deshalb kann man wohl ein CLD auf Flussfaktoren anwenden und dieses dann auch genau so wie oben interpretieren. Aber auch dann muss ich ja diese Unterscheidung vornehmen, da ich ganz explizit jeden Faktor als Flussfaktor interpretieren muss.
Möchte man dies nicht, also ausschließlich Flussfaktoren modellieren, dann muss strenger formuliert werden. Hier nehme ich mal ein anderes von Dir genanntes Beispiel. Eine Erhöhung (Minderung) des Zinsflusses, ergibt ein Kapital, das größer (kleiner) ist als wenn sich der Zinsfluss nicht geändert hätte.
Und mit dieser konkreten Ausdrucksweise nimmt man wieder eine Unterscheidung in Bestand und Fluss vor.
Du siehst also, egal wie ich es drehe oder wende. Ein CLD ohne Betrachtung von Bestand und Fluss ist nicht nur ungenau, sondern kann zu falschen Erkenntnissen führen.
Und nun noch ein bisschen philosophischer. In dem Moment, wo man den zu modellierenden Systemen die Zeitkomponente nimmt, nimmt man ihnen auch ihre Geschichte und damit ihre Lebendigkeit.
Im Sinne Heinz von Försters geschrieben kann man ohne eine Unterscheidung in Bestand und Fluss nur triviale Maschinen modellieren, keine nichttrivialen.
Die Elemente in dem Modell ändern sich dann nicht auf Basis ihrer Geschichte, sondern einzig und allein aus dem Hier und Jetzt heraus, also ausschließlich auf Basis äußerer Signale.
Damit wird das zu modellierende System aber bis zur Unkenntlichkeit trivialisiert. Es wird „getötet“. Also ist für mich auch dieser Schritt als erster kein zulässiger.
Und ganz konkret. Wenn ich Aussagen eines Modell durch einfach nachvollziehbare Empirie revidieren kann, dann ist es nicht passfähig. Und solch eine Aussage ist: „Je weniger Zinsen desto weniger Kapital.“
Daran erkennt man, wie die fehlende Geschichte in den Faktoren zu falschen Aussagen verleitet. Und die Geschichte inkludierst Du durch Hinzunahme der Zeit, in dem Du Unterscheidungen vornimmst in Bestand und Fluss.
BG, Conny
Aber ich glaube, wir sind mit unseren Gedanken relativ dicht beisammen. Und na klar, zusammen würden wir famose Dinge modellieren. 🙂
Danke noch einmal für diesen Beitrag und dafür, dass Du mich zum scharfen Denken angeregt hast.
Hallo Peter,
ich nehme den Ball mal wieder auf, denn ich glaube erkannt zu haben, was in meinem blinden Fleck unserer Diskussion lag, obwohl Du es geschrieben hast: „Die Zeit wird festgesetzt. Es wird ein bestimmter Zeitpunkt betrachtet, kein Zeitraum.“
Dazu habe ich Anmerkungen. Wir nehmen also in der Analyse eines CLDs die Zeit heraus. Alleine das ist schon schwer, aber trotzdem machbar für mich, zu denken, denn Zeit und Raum sind notwendige Kategorien unseres Denkens, gerade, wenn es um Veränderungen geht. Veränderungen geschehen stets in Zeit und Raum. Alleine diese richtige Analyse erfordert viel mathematisches Verständnis, wahrscheinlich noch mehr als Modelle in Bestand und Fluss zu erstellen. Denn die CLDs kommen so scheinbar einfach daher, verleiten aber ohne dieses angeführte mathematische Verständnis zu Fehlinterpretationen. Dann lieber doch gleich am Anfang beim Erstellen des Modells die Hürde hoch setzen, oder?
Jetzt habe ich aber immer noch einen Haken. Vielleicht hilfst Du mir. In dem Moment wo ich Schleifen betrachte, führe ich doch notwendig die Zeit, besser einen Zeitraum, wieder ein, oder? Wie kann ich aufschaukelnde oder ausgleichende Schleifen betrachten, ohne die Zeit zu inkludieren? Das kann ich nicht denken.
BG, Conny
Jetzt bringst Du mich in Verlegenheit. Habe ich tatsächlich geschrieben, dass ich keinen Zeitraum betrachte? Ich finde diesen Passus in meinem Text gerade nicht.
Hast Du 10 Minuten Zeit? Meine Antwort umfasst wenige Zeichen mehr als 280. 🙂
Darf ich nochmals den Kapital-Zins-Loop bemühen? Grundsätzlich ist so ein Loop ja selbstbezüglich. Excel würde reklamieren, wenn man so etwas direkt in Excel abbilden möchte. Wir müssen also irgend eine zusätzliche Denkebene einfügen, um so einen Loop zu verstehen. Dazu nehme ich nur kurz eine Anleihe bei der quantitativen Betrachtung auf. Wenn wir dann den CLD-Loop verstanden haben, vergessen wir alles Quantitative im Zusammenhang mit CLD sofort wieder!
Der Pfeil Kapital –> Zins macht uns ja keine Mühe. Er bildet die Menge der möglichen Kapitalwerte auf die Menge der Zinswerte ab. Einem Kapitalwert K wird der Zins Kp/100 zugeordnet, wobei p eine Zahl zwischen 0 und 100 ist und gemeinhin „Zinssatz“ genannt wird. Genau genommen ist das Kapital eine Funktion der Zeit, also K=K(t) und z(t)=K(t)p/100 wird ebenfalls zu einer impliziten Funktion der Zeit. Hier macht es kein Problem, wenn wir die Funktion einfach zu einem bestimmten Zeitpunkt betrachten, also die Zeit festhalten. Die Zeitabhängigkeit spielt in der Monotoniebetrachtung keine Rolle.
Die Crux ist der Pfeil Zins –> Kapital. Quantitativ sieht diese Funktion so aus: z –> z + K. Wenn wir hier die implizite Zeitabhängigkeit in die Notation einfügen, manifestiert sich die Rückbezüglichkeit: z(t) –> z(t) + K(t). Das ist ja natürlich nun nicht wieder K(t). Richtig wäre: K(t+1) = z(t) + K(t). Hier findet also ein Zeitshift statt! Hier bewegt sich etwas!
Jede Umdrehung im Kapital-Zins-Loop ist ein Zeitschritt! Darin manifestiert sich die Zeit! Der Loop ist gar kein geschlossener Loop, sondern eine Spirale, die in jedem Zeitschritt eine Ebene höher steigt: K(t-1) –> K(t-1)p/100 = z(t-1) –> z(t-1) + K(t-1) = K(t) –> K(t)p/100 = z(t) –> z(t) + K(t) = K(t+1) –> K(t+1)p/100 = z(t+1) –> z(t+1) + K(t+1) = K(t+2) –> …
Für die Monotoniebetrachtung der Abbildung z(t) –> z(t) + K(t) = K(t+1) darf aber die Zeit keine Rolle spielen, denn wir wollen eine Abbildung der Zinswerte untersuchen, nicht eine Abbildung der Zeit.
„Je grösser der Zins heute, desto grösser das neue Kapital morgen“ und „Je kleiner der Zins heute, desto kleiner das Kapital morgen“. Wenn der Zins im Extremfall Null ist, dann ist das Kapital morgen minimal, nämlich unverändert gleich dem Kapital heute. Es nimmt nicht zu, es wächst nicht an.
Du siehst, dass ich mir immer noch Gedanken über CLD mache. Ein MOOC letzten Winter über Applied Category Theory hat mir neue Impulse gegeben. Ich glaube, dass ich den formalen Teil der CLD ganz gut im Griff habe. Probleme macht ja eher die Beliebigkeit, mit der CLD entwickelt werden. Z.B. kannst Du im Kapital-Zins-Loop auch argumentieren, dass der Zins(satz) vom Wert des Geldes abbhängt, d.h. von einem zinsgenerierenden Potential.
Mal ohne in die Sinndiskussion von Zins einzutreten, die Du an einem anderen Ort begonnen hast, könnte ein Modellierer so argumentieren: wenn ich Dir Geld leihe, dann könnte ich ja damit auch etwas kaufen, an dem ich Freude habe, muss jetzt aber meine Wünsche zurückstecken. Wenn Du mir dann das Geld zurück gibst, dann wird das. was ich kaufen möchte, vielleicht teurer sein, darin begründet sich der Zins. Seine Höhe hängt aber von der Kaufkraft des Kapitals ab. Also modelliert er drei Variablen: Kapital –> Kaufkraft –> Zins.
Ich versuche nun, CLD so zu straffen, dass sie eindeutig werden. Das ist schwierig. Dann will ich Tom Fiddamans Einwand, dass „Eroding Goals“ und „Escalation“ mathematisch ununterscheidbar seien, entkräften. Das Programm ist so umfangreich, dass ich mehrere Jahre daran arbeiten muss (und es vielleicht nie zu Ende bringen kann). 🙁
Wie es meine Art ist, dazu noch einen Literaturhinweis. Ich bin kürzlich auf einen Artikel aus einem Springer Konferenzband gestossen und kaufte ihn für 30 Euro: Gullermina Cledou und Shin Nakajima, A Net-Based Formal Framework for Causal Loop Diagrams, 2019.
M.E. basiert die Diskussion in der SD-Community (entweder CLD oder Stock-Flow-Modelle) im Wesentlichen auf der Annahme, dass ein Methodenbruch zwischen beiden Ansätzen besteht. Hiermit haben wir uns bereits vor 15 Jahren intensiv beschäftigt und mit dem iMODELER ein Werkzeug entwickelt, das beide Ansätze vereint. CLDs sind sehr wirkungsvoll – jedoch nur, wenn man diese „methodisch-sauber“ erstellt (hierfür nutzen wir die einfache KNOW-WHY-Fragetechnik, um die direkten Abhängigkeiten systemisch zu definieren) und auch Erkenntnisse hieraus ziehen kann. Und Letzteres geht nicht ohne Software-Unterstützung: Laut einer Studie der University of Queensland können wir im Kopf nur das Zusammenspiel von max. 4 Faktoren überblicken (http://www.innovations-report.de/html/berichte/studien-analysen/bericht-41509.html). Wir verfügen also über mentale Grenzen. Ein CLD ohne Analysemöglichkeit unterstützt dann lediglich die Kommunikation untereinander aber nicht den Erkenntnis-Gewinn. Mit unserem iMODELER können die CLDs grob gewichtet werden. Anschließend zeigt die Erkenntnis-Matrix auf, was für ein erfolgreiches Handeln zu berücksichtigen (z.B. Risiken) und was zu tun ist (z.B. effektivste Maßnahmen). Wie dies geht, zeigen die Videos unter: http://www.consideo.de/Software.html
Dort ist auch zu sehen, wie ein qualitatives CLD oder Teile davon anschließend optional quantifiziert und simuliert werden können und zwar ohne hierfür die komplizierte Stock-Flow-Syntax anwenden zu müssen. Wir sind überzeugt davon, dass gerade die komplizierte Stock-Flow-Syntax die Ursache dafür ist, dass SD sich immer noch in der Nische befindet.
Modelle müssen vielmehr natürlich-sprachlich erstellt werden können und es dürfen dabei auch keine Methoden- oder gar Medienbrüche entstehen.
Das ist richtig. Hingegen sehe ich keinen Methodenbruch zwischen CLD und stock-flow-Diagrammen, im Gegenteil! Für mich ist ein CLD so etwas wie ein Draft eines stoc-flow-diagramm. Ich erstelle jeweils meine stock-flow-diagramme aufgrund eines vorher aufgenommenen CLD.
i wonder how this related to other formalisms like petri nets or https://johncarlosbaez.wordpress.com/ (category theory).
some of it look like it would be treated with coupled differential equations.
Yeah! This is the right question! I’m actually do some research in this direction. I know John Beaz‘ work but don’t think that this could help me. Also I think that the way Baez constuct a category of diagrams isn’t natural. In his interpretation a CLD consisting of some loops would be a morphism from the empty set to the empty set, and this makes no sense. However I’m looking for a category of loops, but has to do some more research. I’m always stumble upon the (Co)homology and am looking in it.
However stock-and-flow diagram are simpler to get a grip on. I have a definition for stock-and-flow-diagrams as a functor category. And then we can possibly apply Beaz‘ functor to the category of differential equations. Intuitively the relation between stock-and-flow diagrams as differential equations is clear.
The appeal of diagrammatic methods is instead of dealing with differential equations (or algebra) you just work with pictures (simplest examples are venn diagrams). However this dream for me is unrealized—i always have to turn the picture back into coupled de’s—this is mostly in chemical reaction networks. Systems dynamics models related to socioeconomic phenomena (eg donnella meadows/world3) often have many more variables.
Baez on his blog also discusses chemical reaction networks. Some papers on physics arxiv also discuss chemical and ecological networks using various formalisms (graph theory, statistical mechanics.) I am only slightly literate in the formalism of category theory—partly because i haven’t seern applications–mostly pure theory.
Well, that’s right. At the end of the day you always go back to DE. However e.g. with managers you cannot communicate in the language of DE. I always started to extract a CLD from their problem descriptions, converted the CLD to a stock-flow-modell and went down to the DE (if needed; the simulation of the stock-flow-modell shows me already the solutions of the DE).
Of course there are applications of category theory, especially on the area of information technology. E.g. the programming language Haskell based on category theory.
Ich sehe hier noch nicht wirklich die Schwierigkeiten: In der Minimalinterpretation sprechen wir von „Kausalität“ und ein Pfeil von X auf Y sagt, dass X bekannt sein muss, um Y zu berechnen (Gegensatz dazu: akausale Modellierung mit DAE – z.B. Elektrotechnik, Physik …). In der Verallgemeinerung könnte man beispielsweise einen DAG benutzen, um ein Bayessches Netzwerk zu beschreiben, d.h. hier hätte man noch Unsicherheit berücksichtigt, weil der funktionale Zusammenhang zwischen X und Y nicht bekannt ist und die Wahrscheinlichkeit des konkreten Wertes für Y BEDINGT zu sehen ist im Hinblick auf den konkreten Wert von X.
CLD und SD sind zunächst deterministisch, aber die Brücke zu Bayes’schen Netzen ist in meinen Augen hilfreich, denn selbstverständlich ist der Übergang fließend, da man in Bayes’schen Netzen auch deterministische Knoten modellieren kann.
Nun kann ein Bayes’sches Netz keine Zyklen (=Loops) enthalten und damit wird deutlich, wo hier die Schwierigkeit liegt: Um sauber zu modellieren, sollte man sich vergegenwärtigen, mit welchem Zeit-Index eine Größe jeweils versehen ist, wenn wir sie abbilden. Wir könnten analog zu einem Bayes’schen Netz auf Indizes verzichten (alles geschieht dann zum selben Zeitpunkt), aber dann muss man Loops als „Simultangleichungssysteme“ verstehen. So werden sie aber nach meinem Dafürhalten niemals verstanden und gerade auch Praktiker denken bei Ursache-Wirkungsdiagrammen an „Prozesse“ und die benötigen praktisch immer Zeit.
Wenn wir aber mit Zeit-Indizes arbeiten, dann ist ein Zyklus(Loop) stets formal auflösbar in eine Aussage der Art:
Y(t+1) := f( Y(t), … )
Das CLD erlaubt nur eine kompakte Notation, die „verschleiert“, dass verschiedene Zeit-Indizes verwendet werden (in der Sprache der Probabilistic Graphical Models und anderer Disziplinen der Informatik sind sie Template oder Plate Models).
Ich denke, man muss hier doch noch auf „Pulsprozesse“ (vgl. Bossel, „Systeme, Dynamik, Simulation“) hinweisen, d.h. wenn wir eine CLD als Wirkungsgefüge betrachten, dann könnte man eine Simulation für ein stets lineares Modell als Pulsprozess definieren ( Y(t+1) – Y(t) := p [ X(t+1) – X(t) ] ) und hier wäre p eine Elastizität („um wieviel Prozent erhöht sich Y, wenn sich X um x% verändert“) für den Pfeil von X nach Y.
Eine andere, einfache Art der direkten Simulation eines CLD besteht darin, eine lineare Funktion der Art Y(t+1) := a X(t) zu unterstellen, hier wäre a als Koppelungsfaktor zu verstehen.
Beides sind nur simple Modelle zu einer ersten Abschätzung der Wirkdynamik, verdeutlichen aber bereits, dass es sehr wohl Unterschiede macht, wie man einen Pfeil von X nach Y „funktional“ interpretiert. Bei einem Pulsprozess sind alle Größen „Bestandsgrößen“ und ein solches CLD müsste ganz anders aussehen, als eines, dass mit Koppelungsfaktoren arbeitet.
Auf Grund des Gesagten würde ich hier klar die Ansicht von Conny Dethloff teilen, dass es hilfreich und m.E. notwendig ist, auch bei Aufbau eines CLD zwischen Bestands- und Flussgrößen zu unterscheiden.
Der fehlende „Doppelpfeil“ verhindert, dass wir den „Zeitsprung“ erkennen, wenn wir in diskreten „DT“ denken. Nur Differentialgleichungen erlauben eben per Definition, die Änderung in einem Zeitpunkt zu beschreiben, oder?
Das ist richtig. Sicher ist ein CLD, das Flussgrössen mit einbezieht, für den Entwicklungsprozess praktischer. Meistens werden Flussgrössen erst im Stock-Flow-Diagramm berücksichtigt. Dort kommt man automatisch zu den Flussgrössen. Beispielsweise wird der grundlegende Motor eines Geschäfts: Verkäufe –> Ertrag –> Marketingbudget –> Kundenbasis –> Verkäufe so übernommen. Die Frage, welches Fluss- und welches Bestandesgrössen sind, stellt sich hier noch gar nicht, denn zunächst ist es wichtig, Feedbackprozesse zu identifizieren. Wenn mal alle wesentlichen Feedbackschlaufen bekannt sind, würde ich dann darauf aufbauend ein Stock-Flow-Modell entwickeln. Da werden dann die Flussgrössen manifest. Im CLD geht es bloss darum, aufschaukelnde und zielsuchende Zyklen zu identifizieren und damit die wirkenden Archetypen zu finden.
Ich verstehe die Frage, ob bei der CLD-Entwicklung bereits Fluss- und Bestandesgrössen unterschieden werden sollen, als eine didaktische. Ich habe oft mit Managementteams CLD entwickelt und hatte den Eindruck, dass die Workshops überladen gewesen wären, wenn ich bereits auf die Unterscheidung gepocht hätte. Bei der anschliessenden Stock-Flow-Modellbildung kommen die Flussgrösse auf eine netürliche Weise hinein.
D’accords. Zunächst sollte man m.E. den SD-Fremden ermöglichen, einen Sachverhalt in der Art und Weise zu beschreiben, der Ihnen geläufig ist. Das Wenn-Dann-Schema („führt zu“) ist sicher hilfreich und es genügt, später dann auf Bestands- und Flussgrößen zu kommen.
Die Doppelpfeile eines Stock-Flow-Diagramms finde ich übrigens hilfreich, da hier die Prozess-Analogie für Flüsse zum Tragen kommt.
Ich muss allerdings gestehen, dass ich zwar die Bildsprache der gekoppelten Feedback-Schleifen, wenn Sie gut gemacht sind, schätze, aber die Nützlichkeit als Erklärungsmittel doch arg beliebig finde: Niemand kann auf Basis eines CLD wirklich zuverlässig erklären, warum und wie sich ein System im Zeitverlauf entwickelt. Letztlich hilft hier doch nur recht aufwändige Mathematik (Loop-Eigenvalue-Elasticity?), da bei nichtlinearen Systemen die dominanten Loops wechseln?
Und das ist vermutlich das immer wieder diskutierte Dilemma: „…die Bildsprache der gekoppelten Feedback-Schleifen, wenn Sie (sic) gut gemacht sind, schätze, aber die Nützlichkeit als Erklärungsmittel doch arg beliebig finde…“. Das ist vermutlich sehr individuell. Wie ich geschrieben habe, kann ich mit CLD sehr viel anfangen. Es zeigt, wo die Motoren des Systems sind und wie diese gebremst werden. Es zeigt auch Fern- und Nebenwirkungen auf, die vielleicht verzögert zuschlagen.
Für Stock-Flow-Fans sage ich: CLD können als Blaupausen von Stock-Flow-Modellen genutzt werden. Das sollte genügen, damit auch sie CLD entwickeln. Ich habe ja aufgrund des Huhn-Ei-CLD verschiedene Stock-Flow-Versionen entwickelt, hier
https://steemit.com/de-stem/@paaddor/wie-kann-man-aus-wirkungsnetzwerken-simulationsfaehige-stock-flow-modelle-bauen
hier: https://steemit.com/de-stem/@paaddor/verbessertes-system-dynamics-modell-einer-huehnerfarm
und hier: https://steemit.com/de-stem/@paaddor/endgueltiges-huehnerfarm-modell-in-als-beispiel-fuer-system-dynamics
und gezeigt, wie auf einem einfachen CLD ganz natürlich alle Flüsse und Hilfsvariablen reinkommen, insbesondere, wenn man noch die Einheiten pedantisch genau mitnimmt.
Wer mit CLD arbeitet (und etwas von Stock-Flow-Modellen weiss), muss sich vom Stock-Flow-Denken völlig lösen. Kreise sind in CLD *echte* Kreise, es gibt in einem CLD ausschliesslich Kreise und weder Bestände noch Flüsse und die Pfeile sind monotone Funktionen zwischen endlichen Mengen und sonst nichts (Y=f(X1, … , Xk) ist ja eben genau eine Funktion!). Das Schema heisst nicht „Wenn-dann“ oder „führt zu“, sondern schlicht „monoton wachsend“ oder „monoton fallend“. Wenn man diese Regeln beachtet, sind CLD mächtige Instrumente zur Abschätzung einer Dynamik.
Akzeptiert, Pfeile sind Funktionen, bei denen jeweils die anderen Einflussgrößen fixiert sind. Da man allerdings bei k Faktoren nicht gerne k Funktionen hinschreiben möchte ist, es einfacher und doch auch gängige Praxis, Knoten als Gleichungen aufzufassen (hier gilt: ein Knoten ist stets eine Gleichung).
Die Anzahl der Loops bei CLD kann allerdings relativ schnell explodieren und nicht umsonst ist das Auffinden eines Hamiltonkreises in einem Graphen NP-vollständig (das Auffinden eines Zyklus ist ja stets equivalent zum Auffinden eines Hamiltonkreises für einen Subgraphen).
Auch wenn die Unterscheidung Bestands- und Flussgröße zunächst nicht relevant ist, entspricht es doch m.E. dem Anliegen der Systemwissenschaft, Systeme auf analoge Strukturen herunterzubrechen (Struktur => Verhalten): Letztlich können sämtliche Zwischengrößen — also enodgene Nicht-Bestandsgrößen — auch in CLD eleminiert werden um kompakte Graphen zu erhalten. Diese Möglichkeit habe ich erst, wenn Bestandsgrößen identifiziert wurden.
Ich halte hier im Ergebnis aus meiner Sicht fest:
1. Ja, CLD sind u. U. geeignete Blaupausen für Simulationsmodelle und näher an der Erfahrungswelt von Praktikern.
2. CLD benötigen zunächst keine Unterscheidung zwischen Bestands- und Flussgrößen; diese ist allerdings hilfreich und ermöglicht kompaktere Darstellungen.
3. Das Auffinden aller Zyklen in CLD ist nicht trivial und explodiert (CLD mit 16 bis 20 Größen führen bspw. bereits zu 200 Zyklen; vgl. die Beispiele in Frank Brand, Komplexe Systeme , 2013).
4. CLD bieten Hilfestellung bei der Identifikation von Eingriffen und wichtigen Stellgrößen und erste Indikation für Stabilitätserwägung; allerdings ist eine Ableitung der Dynamik des beschriebenen Systems im Zeitverlauf zuverlässig nicht möglich. Der Verzicht auf weitergehende Modellierung (SFD) bedeutet doch letztlich die trügerische Annahme, man „wisse“, die tatsächliche Dynamik sei für das Problem unerheblich. CLD bergen insofern m.E. die Gefahr einer trügerischen „Kontroll-Illusion“.
Richtig! Genau das ist der springende Punkt: Zyklen werden nicht aufgesucht, sondern gemacht! Sobald man einen Pfeil A –> B hat, ist das einzige Bestreben, einen Pfad von B nach A zu finden. Wenn der Kreis geschlossen ist, zeichnet man weitere Kreise, die mit dem ersten verbunden sind. Pfeile, die nicht in Kreisen sind, können weggelassen werden, denn sie sind nullhomotop.
Ich habe die Managementteams, mit denen ich CLD entwickelt habe, zuerst gefragt, welches der Motor ihres Geschäfts sei. Ein „Motor“ ist ein aufschaukelnder Kreis, üblicherweise kam da jeweils: Verkäufe –> Ertrag –> Marketingbudget –> Marketingmassnahmen –> Kundenbasis –> Verkäufe. Ein Kreis enthält fast nie Flussgrössen. Wenn die Kunden z.B. zwischen Marketingmassnahmen und Kundenbasis noch eine Beschreibung des Flusses neuer Kunden hätten einbauen sollten, wäre mein Mandat schnell beendet gewesen, den das interessiert hier nun einfach noch nicht.
Ich weiss, dass es Lehrbücher gibt, die eine chaotische Entwicklungsweise von CLD propagieren. Dadurch habe ich schon Berater gesehen, die mit ihren Kunden wild drauf los zeichneten und völlig unübersichtliche und wenig hilfreiche CLD machten, in denen die Kreise nicht explizit sichtbar gemacht waren.
Auch Stock-Flow-Modelle bergen die Gefahr einer Kontrollillusion, wenn der Entwickler zu wenig vertraut mit System Dynamics ist, denn System Dynamics hat nicht den Anspruch von Systemkontrolle. Weder ein Stock-Flow-Modell, noch ein CLD haben das Ziel, Kontrolle auszuüben. Das Ziel eines System Dynamics Modells, sei es ein CLD oder ein Stock-Flow-Diagram, ist das Entwickeln von Policies.
Ja, das sehe ich auch so. Auch ich sehe keine Schwierigkeiten. In der Tat ist ein Zyklus eigentlich eine Helix. Nach jeder Umdrehung ist man ein „Zeitstockwerk“ höher (oder tiefer).
Die Beschreibung „ein Pfeil von X auf Y sagt, dass X bekannt sein muss, um Y zu berechnen“ scheint mir ein wenig verwirrend. Ein Pfeil von X nach Y ist eine Funktion, die jedem Wert von X einen Wert von Y zuordnet, unter Umständen aber eben unter Berücksichtigung eines Zeitschubs um den Faktor plus oder minus 1.
CLD und Stock-Flow-Modelle brauchen nicht unbedingt deterministisch zu sein. Normalerweise sind die Grössen stochastisch modelliert.
Über den Zusammenhang zu Bayessche Netze habe ich auch schon nachgedacht, aber noch nicht ganz verstanden, wie das geht. Ein Bayesnetz ist ein zyklenfreier gerichteter Graph, während ein CLD grundsätzlich ausschliesslich aus Zyklen besteht.
Wenn man das Modell kompakt schreibt (Hilfsgrößen wurden eleminiert, wir nutzen Vekoren/Matrizen etc.), würde ich die Äquivalenz Pfeil = Funktion (spezielle Relation) sehen, aber in der allgemeinen Form nicht zwingend, weil für mich ein Knoten in einem solchen Graphen als Gleichung interpretiert werden kann und die „rechte Seite“ dieser Gleichung aus mehreren Komponenten bestehen kann, z. B.:
Y = f ( X1, X2, … , Xk )
Im CLD gäbe es in diesem Fall doch k Pfeile, aber nur eine Funktion, die im nichtlinearen Fall nicht zwingend in k Operatoren separierbar sein muss, oder übersehe ich hier etwas?
Das Bayessche Netz ist m.E. auf SD übertragbar, wenn man mit festem Zeitschritt arbeitet, da dann eben keine echten Zyklen auftreten. Wenn man mit festem Zeitschritt in SD arbeitet, dann sollte man mit dem Instrumentarium der Probabilistic Graphical Models auch in SD sehr weit kommen, in Ansätzen wird dies doch m.E. bei MCMC/Partical Filtern auch so gemacht?
This is a sort of irrelevant query by someone who has only a sort of basic understanding of system dynamics, networks, and related ideas (petri nets, ‚logic diagrams‘ (C S Pierce, laws of form, knots..), ecological, economic and chemical reaction networks, feynman and cluster diagrams.. but i just wonder
1) whether and how all these models are related –that might take a PhD level book
2)the above CLS formalism in anyway particularily useful for things like ‚multiobjective optimization ‚ (like budgeting—with N dollars how do you spend it to get M things that wuill make you happiest. Or if you have a ‚team‘ of N people with different talents/skills or different amounts of money, how do you assign them to tasks and spend the collective money to optimally solve some common problem.
(I’m partly thinking about things like science funding—-
peopple have N tax dollars and M scientists with different skills, and you have say K possible research projects whose outcomes are uncertain in various ways. My area has a debate or duispute now over whether people should support a carbon tax, or something else, and whether to spend time on politics–passing a law—or instead on businesses making solar energy easy to get.
The canonical example in economics is to use calculus of variations—lagrange multipliers. But there are many other approaches.
also wonder if there are any reccomendations for simple, less technical examples of how CLS is used. In other words, something like a recipe or introductory textbook book for decisionmaking.
Thank you for this informative comment. As a mathematician who has been involved with System Dynamics for over 20 years and as a longtime member of the System Dynamics Society, I understand well what you mean, and also I understand that you mess things up.
The title of my article is based on the paper I quoted from Tom Fiddaman. I do not think he just has a basic understanding of system dynamics, networks, and related ideas because he was at least once president of the System Dynamics Society. The discussion about CLD has been taking place in relevant circles for almost 40 years now and is by no means an irrelevant query. But you may not be deep enough in the System Dynamics Scene to know about it.
Yeah–thanks. I really only know systems dynamics from books by D Meadows, and old ones by J Forrester, but never really studied it in detail. Also the little modeling i’ve done was mostly paper and pencil not simulations. The paper /pencil stuff often is not really applicable except conceptually –they are ‚toy models‘ like random walks , cellular automota, urn models, etc in physics. I’m actually equally interested in comparative stuff , history and philosophy of science and modeling.
There was a paper in 2014 by Safa Motesharrie of U. Maryland on ‚civilizational collapse‘ which seemed to borrow from both systems dynamics and mathematical ecology–the sort of thing i am more familiar with.